第四部分：函数与程序的模块化设计

一、函数概述

利用之前学过的 C 语言语法，我们已经可以编写一些简单的程序了，但如果面对一些复杂的程序问题，如果将所有代码全都写在一个主函数里，会显得程序特别繁琐，没有可读性。例如我们想做一个简单的计算器，可以进行四则运算和三角函数、开方平方等运算，这个时候就需要有一种“组装”的思想，将每一个功能单独编写，然后在主函数中分别调用。这就涉及到 C 语言中“模块化程序设计”的设计思想。

在设计较大的程序时，往往将整个程序分为很多程序模块，分别写在对应的函数中，每个函数实现一个特定的功能。一个函数可以被其他函数调用多次。在一个程序中，只能有唯一的一个 main 函数。

我们举个例子来体会一下模块化程序设计的思想，例如我们想要写一个程序，可以输出在两个星号间的字符：

#include<stdio.h>
void charwithstar(char s)
{
    printf("**********\n%c\n**********" , s);
}
int main()
{
    void charwithstar(char s);
    charwithstar('c')
    return 0;
}

这个程序的运行结果是：

**********
c
**********

上述程序中，charwithstar 是用户自己定义的一个函数，功能是输出一个夹在两行星号间的字符。在函数这一部分，有一些名词的概念需要明确。

• 参数：定义函数功能时用到的变量，用来指定函数的相应功能。例如add是我们定义的一个函数，它的功能是将 a 和 b 相加，那么a和b就是这个函数的参数。

• 返回值：函数的所有功能进行下来，需要保留到调用函数的函数中使用的值。比如刚才的add函数，我们需要将 a 和 b 的值加起来进行赋值，那么 a 和 b 的加和就是这个函数的返回值，就是整个函数的值。

C 程序从 main 函数开始，遇到其他函数时跳转到对应函数，执行完对应功能后回到 main 函数，最后在 main 函数中结束整个程序。函数与函数之间互相独立，不可以嵌套定义。从函数形式看，函数分为有参函数与无参函数。无参函数一般用来执行固定的操作，有参函数一般需要进行参数传递，对不同的参数进行处理输出。函数有的带回返回值，有的不带回返回值，这个因程序而异。

二、函数的定义

定义一个函数即告诉编译系统你想要定义的函数的名字、功能、返回值类型、参数名字与类型，这样编译系统才能定义一个你期望功能的函数。通常定义一个函数的一般形式为：

返回值类型名  函数名(参数类型名 参数名, 更多参数……)
{
    函数体
    ……
    指定返回值
}

其中，如果没有参数，可以不写参数或者在参数的位置写 void，如果没有返回值，可以在返回值类型名的位置写 void。我们甚至可以用以下的方法来定义一个空函数：

void empty()
{ }

这是一个空函数，它什么也不做。在程序的实际设计中，往往需要在设计程序的最开始写好程序的大纲，这个时候就需要把每一个能想到的功能用空函数的形式写在指定的位置，这样做的话程序结构清晰，对日后的修改有益。

特别地，我们指定 main 函数的返回值是 int 型，在 main 函数末尾要让主函数返回0作为函数执行完毕的标志。有的参考资料中规定 main 函数是 void 型，此时 main 函数末尾不需要返回 0。这个因教材而异，在这里我们统一规定为前者。

三、函数的声明与调用

定义一个函数当然是为了在其他位置使用这个函数。调用函数之前，必须要事先声明。这里的声明包括函数事先在预处理行中包含进去的情况，此外，需要自行定义。例如我们在程序开端定义了一个函数：

int add(int a, int b)
{
    return a + b;
}

它的功能是将 a 和 b 两个数相加。然而我们在 main 函数中调用这个函数的时候需要再声明一次：

int main()
{
    int add(int a, int b);
    printf("%d" ,add(1, 2));
    return 0;
}

可以看到，在第 3 行类似将函数原型，只是多了一个分号，这就是函数的声明。函数在调用之前必须要进行声明。

函数调用的一般形式为：

函数名(实参表列)

如果函数没有参数，可以省略实参表列，但括号必须有。函数有三种调用方式，其一是单独调用，一般用来实现一些操作；其二是作为函数表达式，函数的返回值作为一个值来使用；其三是作其他函数的参数。其二和其三实际上属于同一种。

函数在调用的时候，涉及“参数传递”的问题。当定义函数时，函数的参数称为“形式参数”（简称“形参”）。当调用函数时，被调用函数的参数称为“实际参数”，（简称“实参”）。调用函数时，实参传递给形参，这个过程叫参数的传递（简称“传参”）。具体过程如下图。

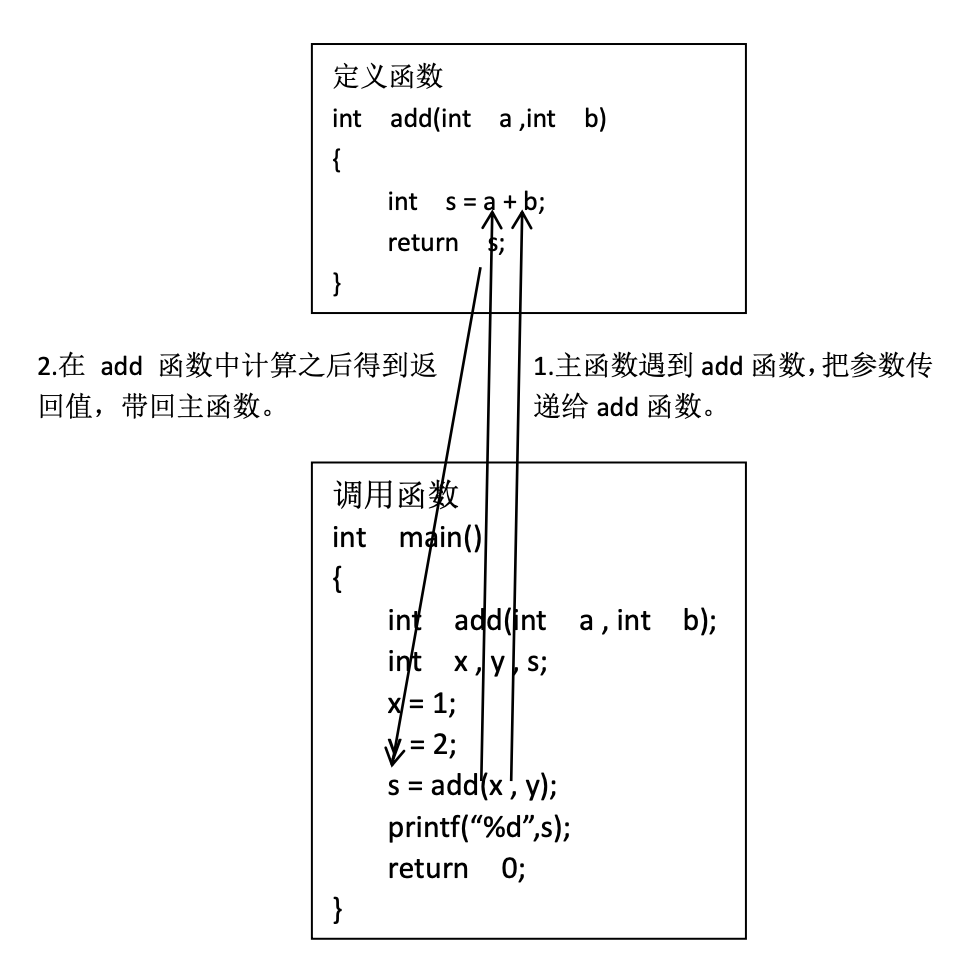
图：函数传递参数示意图

函数在调用的时候可以互相嵌套，就是将一个函数的返回值作为下一个函数的参数。例如 add 函数是两个数相加，multi 是两个数相乘。那么

add(multi(a, b), multi(c, d));

则表示数学算式：

a * b + c * d

这就是函数的嵌套使用。

四、函数的递归调用

在一个函数中直接或间接调用其函数本身叫做函数的递归调用，这是 C 语言的一大特色。例如下面这个求 n! 的数学函数：

$$f(x)=\{\begin{array}{l}{x}^2,x\ge 0\\ -x,x<0\end{array}$$

当我们求一个数的阶乘时，可以将问题转化为 n * (n - 1)! 的问题，这样的话这个问题就转换成了一个经典的递归问题。例如我们要求 fac(3)：

fac(3) = 3 * fac(2)
fac(2) = 2 * fac(1)
fac(1) = 1

fac(2) = 2 * 1 = 2
fac(3) = 2 * 3 = 6

这样就完成了整个递归算法。这里我们可以发现，所有递推式都可以化为递归。一个递归问题分为两个部分，分别是递推与回归。由已知的结果递推，推到有已知值的式子之后再向原方向回归，最后得知结果。又例如下面这个求斐波那契数列第n项的函数：

int fib(int n)
{
    if(n == 0) return 0;
    if(n == 1) return 1;
    if(n >1) return fib(n - 1) + fib(n - 2);
}

在求解过程中，求 fib(n) 的时候就要推到求解 fib(n - 1) 和 fib(n - 2) 的问题上，这样就又必须计算 fib(n - 3) 和 fib(n - 4) ，以此类推，最后将会推到 fib(1) 和 fib(0)，能立即得到结果。这时候递推终止，再一路返回到 fib(n) 的值。这样看来，递归一定要有结束条件，否则就是一串无止尽的循环。

递归运算的优点是源程序简洁，缺点也很显著，会消耗过多的内存与运行时间，效率不高。

五、局部变量与全局变量

我们最常见的定义的变量都是在 main 函数中定义的，它们在整个 main 函数中都有效。也有的变量定义在我们自己定义的函数里，有没有想过，在其他的函数里可以使用这个变量吗？答案是不可以的。这就是变量作用域的问题。

定义变量时有三种情况：在函数外部定义、在函数开头定义、在函数中定义。在函数中复合语句内定义的变量只能在复合语句中使用能够，在函数开头定义的变量可以在整个函数内使用，这两种变量叫做“局部变量”。在函数外部定义的变量可以在整个程序中使用，这种变量叫做“全局变量”。例如有以下示意程序：

int m, n;
func_1(int a)
{
    int b, c;
    ……
    {
        int i, j;
        ……
    }
    ……
}

在上述程序全部定义的变量中，m、n 是全局变量，可以在整个程序中使用。b、c 是函数 func_1 的局部变量，只能在这个函数中使用。i、j 是复合语句（5 ~ 8行）中的局部变量，只能在这个语句块（一个花括号内）中使用。

六、变量的声明与定义

因为变量的作用域不同，而我们有时候需要调用一些本来不在此作用域中的变量，就需要对已经定义好的变量进行声明。例如在如下的示意程序中：

int m, n;
func_1(int a)
{
    int b, c;
    {
        int i, j;
        ……
    }
    ……
}
func_2(int d)
{
    int e;
    ……
    extern b;
}

在第 15 行我们用 extern 关键字将变量 b 声明，这样我们就可以在 func_2 函数中使用变量 b。使用 extern 关键字声明变量意味着我们将此变量的作用域扩展到此。